
うげ、、、
数学は苦手です。ブログ退出させてもらいます・・・

ちょっと待ってください!
この記事ではその中でも面白そうな部分だけ取り上げて話をします!
ロジカルシンキングに繋がる部分でもあるので、少しお付き合いください!
この記事でわかること
- みんなが勘違いしている「数学」
- 公務員試験でも役に立つ「これ数学?」
- 数学は「具体化と抽象化」
今回の書籍
今回の書籍テーマは『考える力をつける数学の本』です。
数学に拒否反応を持っている方こそ一度読んでみてください。私も根っからの文系であり、読み飛ばしてしまうところも多々ありましたが、それでも価値のある書籍です。
中古だと24円から買えます(笑)
「数学」とは
理系文系といわれるように「数学」が得意な人はすごい・・・自分ではできない。
といった苦手意識を持っている方も多くいらっしゃると思います。
著者の岡部さんも数学には「狭い数学」と「広い数学」があると説明しています。
誰でも役に立つのは「広い数学」です。
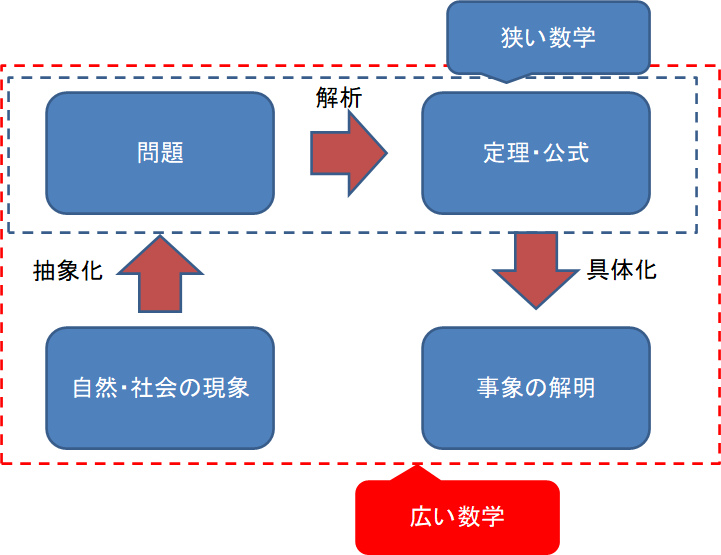
広い数学は公務員試験でも
トイレットペーパーの長さを算出するなど、生活を例に書籍の中では解説していますが、最も数学っぽくないものを話してみたいと思います。
問題1
[問題]
A,B,Cの3人がいます。このうちの1人だけが正直者で、あとの2人はウソしか言いません。
本文からの引用
この3人に誰がウソつきかをきいたところ、次のように答えました。では、正直者は誰でしょうか。
A「Bはウソつきだ」
B「Aこそウソつきだ」
C「Bはウソをいわない」
いかがでしょうか?考えてみてください。
答え
正直者は「A」です。
解き方
3人のなかで共通して、同じ人のことを言っている場合、同じことを言っていなければどちらかがウソつきでどちらかが正直者になります。
今回はBのことをAとCが「ウソツキだ」「ウソをいわない」と矛盾しているため、どちらかが正直者とわかります。
そうするとBがウソツキであることは確定です。
そうするとBはウソ(反対のことを言っており)「Aこそウソつきだ」→「Aこそ正直(反対なので)だ」となりAが答えとなります。
ひとつひとつに着目するとかなり面倒な感じがすることも全体をみて共通項を探していけばかなり楽になっていきます。
これは「A=B」「C=B」ならば「A=C」という処理を文面で行っているのです。
この解き方が数式を使うのか、どうか・・・ということです。
こんな問題が結構たくさんあります。
問題と答えだけ載せますので、解き方が気になる方は本書を手に取ってみてください。
問題2
A〜Eの5人が、宝くじを買ったところ、1人だけあたりました。
本文 地方公務員上級試験からの引用
あとで5人に話を聞いたところ、次のような返事が返ってきました。
A「当たったのはCだ」
B「当たったのはAだ」
C「Aは『Cがあたった』と言ったが、それはウソだ」
D「私は当たっていない」
E「あたったのはBだ」
しかし、本当のことを言ったのは5人のうち1人だけで、他の人はウソをついています。
では、宝くじが当たったのは誰でしょうか。
答え
正直者は「D」です。
問題3
ある事柄に関して、A、B、Cが次のような申し立てをしました。
A「私はしていない、Bもしていない」
B「私はしていない、Cもしていない」
C「私はしていない、誰がやったか知らない」
このとき、3人とも発言の半分は本当で半分はウソを言っていたとすると、この事柄をしたのは誰でしょうか?選択肢 1:AとB 2:BとC 3:A 4:B 5:C
本文 地方公務員上級試験からの引用
答え
正直者は「4:B」です。
数学とは「具体化」と「抽象化」
広い意味での数学とは具体化と抽象化です。
これは日常の問題解決にほかなりません。
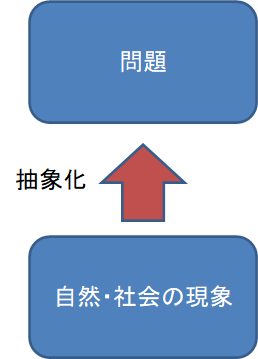
例えば、これを中小企業診断士の試験に例えるのであれば、事例Ⅰの問題などで
「成果主義を導入したところ業績が下がった。この要因は何があるか」
という問題があったとすると
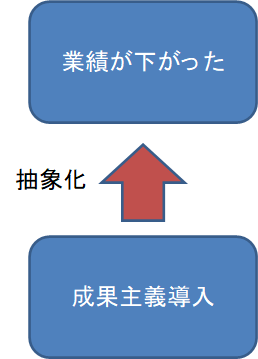
これを次のプロセスに進めていきます。

そうすると従業員に聞くと以下のような現実がわかりました
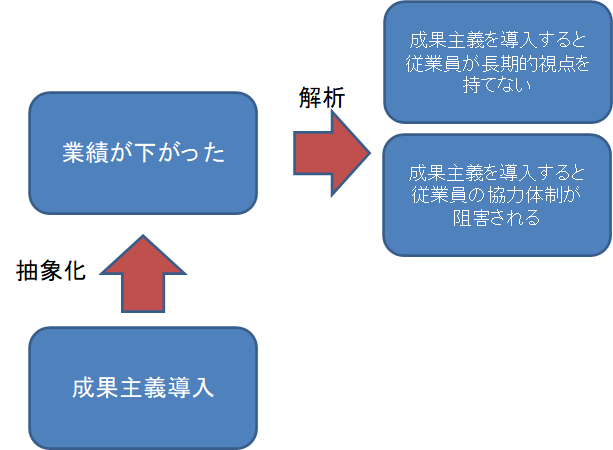
これを具体化すると以下のようなことが考えられるのです。
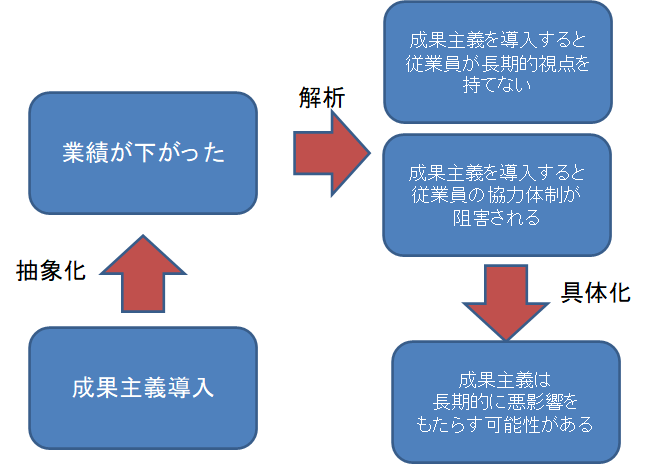
言われてみればそうだな・・ということもこう考えてみると面白いですね。



コメント